تاریخچهی اجسام افلاطونی

سنگهای کوچک کندهکاری شده در اسکاتلند که از عصر نوسنگی بهجا ماندهاست، نشان میدهد که بشر تقریبا 1000 سال پیش از افلاطون، چندوجهیهای منتظم را میشناخته و به شکل متقارن آنها علاقهداشته است. شواهدی نیز وجود دارد که نشان میدهد مصریان باستان از این احجام در معماری خود بهرهمیبردند؛ هرمهای غولپیکر، بارزترین نمونهها هستند. اما یونانیان باستان، دربارهی این اشکال بحثهای فراوانی انجام دادند. اقلیدس در رسالهی هشتم خود دربارهی سهتا از این اجسام بحثهایی انجام دادهاست. افلاطون در یکی از نوشتههای خود این حجمهای منتظم را به عناصر سازندهی جهان مربوط دانستهاست: چهاروجهی به آتش، ششوجهی به خاک، هشتوجهی به هوا، بیستوجهی به آب و دوازدهوجهی به کل جهان هستی اختصاص دارد. شاید همین توضیحات افلاطون سبب شده تا این پنج حجم به نام او شناختهشود. یونانیان باستان تا سالها پس از اقلیدس و افلاطون همچنان بهدنبال ریاضیات حاکم بر این حجمها بودند؛ در سدهی 6 میلادی در کتابی با نام کتاب پانزدهم اقلیدس (که البته اقلیدس آنرا ننوشته است!) دربارهی روش محاط کردن این اجسام در یکدیگر، تعداد رئوس و زاویهی میل وجوه همسایه بحث شدهاست. نمونههایی از این مسایل را میتوانید در جلد اول کتاب "آشنایی با تاریخ ریاضیات" نوشتهی هاوارد.د.ایوز ببینید. در قرن 16 میلادی، یوهان کپلر منجم بزرگ آلمانی که علاقهی بسیاری به یافتن روابط جادویی میان اعداد داشت، براین باور بود که میتواند شعاع مدار سیارات منظومهی شمسی را با کمک نسبت حجم اجسام افلاطونیای که برهم محیط شدهاند بیابد. او مدلی برای توضیح محاسبات و نظر خود ساخت، اما تنها دلیلاش برای این باور و حدس، نظم بسیار زیاد چندوجهیهای منتظم بود که به آنها حالتی افسانهای میداد. او پس از صرف وقت بسیاربرای اندازهگیری اطلاعات مداری سیارات، به روشهای علمی رویآورد؛ بهاینترتیب توانست سه قانون بسیار معروف خود را دربارهی مدار و حرکت سیارات منظومهی شمسی صورتبندی کند.
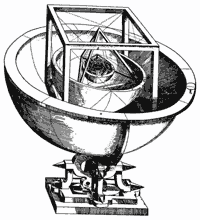
مدل اولیهی کپلر برای منظومهی شمسی
بالاخره در قرون 16 تا 18 میلادی، ریاضیدانهای بزرگی چون دکارت، کوشی، اویلر و لژاندر توانستند اثباتهایی برای وجود تنها پنج چندوجهی منتظم ارایه کنند. از قرن 18 میلادی به بعد در شاخهای جدید از ریاضیات بهنام نظریهی گروهها، بحث اندازهگیری میزان تقارن چندوجهیهای منتظم و غیرمنتظم، و معرفی انواع تقارن آنها آغاز شد.