کلاس هندسه در جزیره
تا به حال آقای ثلاثی توانسته بود مسئلههای زیادی را که برای ساکنین جزیره حل نشده بود، حل کند و طی حل این مسائل، هفت اصل برای هندسهاش پیدا کند. ولی مشکلی در این بین وجود داشت. هر چند که اهالی جزیره در تا کردن مهارت داشتند، ولی چیزی از هندسهی اقلیدسی نمیدانستند و این باعث میشد آقای ثلاثی نتواند راه حلهایش را در مورد مسئلههای مربوط به تا کردن برایشان توضیح دهد. به همین خاطر آقای ثلاثی بیآن که بتواند در مورد هر مسئله قاعدهای کلی بدهد که چه زمانهایی میشود تای خاصی زد و چه زمانهایی نمیتوان، مجبور بود هر بار یک برگ خاص را ببیند و بعد با استفاده از قاعدهی کلی خودش در آن مورد خاص هم جواب بدهد. این بود که روز به روز مشاوره به طراحان وقت بیشتری از او میگرفت. برای همین یک روز آقای ثلاثی به رئیس جزیره پیشنهاد داد در دورهی کوتاهی به تعدادی از جوانان جزیره مقدمات هندسهی اقلیدسی را آموزش بدهد، تا آنها هم بتوانند بخشی از کار آقای ثلاثی را انجام دهند. این پیشنهاد با موافقت سرشار از خوشحالیِ رئیس جزیره مواجه شد.

خیلی زود کلاس هندسه در جزیرهی اریگام برگزار شد. شاگردان کلاس از قبل به خوبی با مفاهیم خط و نقطه آشنا بودند. فاصله مفهومی بود که برایشان واقعاً مفید بود ولی به این شکل با آن آشنا نبودند. بعد از آشنایی با آن، دایره و سهمی و شکلهایی را که از خطهای راست ساخته نمیشدند شناختند. خیلی زود مقدمات مورد نیازشان را از هندسهی اقلیدسی فراگرفتند. حالا نوبت به کار بردن این دانستهها در هندسهی کاغذ و تا بود.
هندسهی کاغذ و تا با این هفت اصل شروع میشد:
۱- از هر دو نقطه روی کاغذ، یک تا میگذرد.
۲- برای هر دو نقطه روی کاغذ، دقیقاً یک تا وجود دارد که آنها را روی هم منطبق میکند.
۳- برای هر دو خط روی کاغذ، حداقل یک تا وجود دارد که آنها را روی هم منطبق میکند.
۴- برای هر نقطه و هر خط روی کاغذ، دقیقاً یک تا وجود دارد که از نقطه گذشته و خط را روی خودش منطبق میکند.
۵- اگر روی یک برگ یک خط و دو نقطهی $p_1$ و $p_2$ داده شده باشد، تایی وجود دارد که از $p_2$ گذشته و $p_1$ را روی خط منطبق میکند.
۶- برای خطهای $l_1$ و $l_2$ و نقاط $p_1$ و $p_2$، تایی وجود دارد که $p_1$ را بر $l_1$ و $p_2$ را بر $l_2$ منطبق کند.
۷- برای خطهای $l_1$ و $l_2$ و نقطهی $p$ روی کاغذ، تایی وجود دارد که بر $l_2$ عمود باشد و $p$ را روی خط $l_1$ منطبق کند.
البته دو تا از این اصول در شرایط خاصی برقرار بودند که بعد از درک مفهوم فاصله، شاگردان کلاس این شرایط را هم به خوبی میشناختند. تا همین جا هم هدف از برگزاری کلاسها برآورده شده بود. ولی رئیس جزیره از آقای ثلاثی خواست همچنان به تدریس در این کلاس ادامه دهد. مسائل پایین صفحه، اولین مسائلی است که آقای ثلاثی به شاگردان خود داد تا آنها را حل کنند:
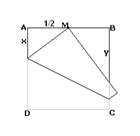
شکل ۱
با تا کردن کاغذ و استفاده از هفت اصل هندسهی کاغذ و تا و دانستههایتان از کلاس درس، مسئلههای زیر را حل کنید.
۱- روی یک برگ پاره خطی را مشخص کنید، سپس آن را به نسبت ۱ به ۳ تقسیم کنید.
۲- مثلثی رسم کنید که هر سه ضلعش با هم برابر باشند.
۳- مستطیل ABCD را در نظر بگیرید، اگر M نقطهی دلخواهی روی ضلع AB باشد، ابتدا تایی بزنید که M را روی C منطبق کند، سپس تایی بزنید که M را روی D منتقل کند، ثابت کنید این دو تا همدیگر را روی عمود منصف ضلع AB قطع میکنند. M
۴- نقطهی وسط ضلع AB از مربع ABCD است، تایی بزنید که نقطهی D را روی M منطبق کند، اگر طول ضلع مربع ۱ باشد، پاره خطهای ایجاد شده روی اضلاع BC و AD از مربع را پیدا کنید.
۵- مثلثی قائم الزاویه رسم کنید که نسبت دو ضلع قائمهاش ۳ به ۴ باشد.