کاغذ و تا، خطکش و پرگار را پشت سر میگذارد؟!
آقای ثلاثی بعد از حل یکی از مسائل حل نشدهی جزیرهی اریگام و گرفتن جایزه از رئیس جزیره، بهعنوان مشاور ارشد طراحان شکلهای کاغذی جزیره منسوب شد و طراحان مشکلات خود را برای طراحی شکلهای جدید با او در میان میگذاشتند. یکی از این مشکلات، دومین سؤالی بود که رئیس جزیره برای جوابش جایزهی دیگری تعیین کرده بود و از مسئلهی اول به مراتب سختتر بهنظر میرسید. سؤال این بود که:
اگر یک نقطه و یک خط قرمز و یک نقطه و یک خط آبی روی برگی داشته باشیم، آیا همیشه می توان تایی پیدا کرد که نقطهی قرمز را روی خط قرمز و نقطهی آبی را روی خط آبی منتقل کند؟
آقای ثلاثی مدت زیادی را صرف جواب دادن به این سؤال کرد. خطها و نقطههای زیادی را امتحان کرد، بیشتر اوقات تایی پیدا میشد که چنین کاری بکند، گاهی هم نه، حتی چند بار توانست دو و یا سه تا پیدا کند که این کار را انجام بدهد. در نهایت جواب مسئله پیدا شد. این بار جواب را با چیزی غیر از دانستههایش دربارهی خط و دایره پیدا کرد. استفاده از سهمیها کلید حل این معما بود. تایی که یک نقطه را روی یک خط منتقل میکند در واقع خطی مماس بر سهمیای است که از آن خط و آن نقطه به یک فاصله است و این نکتهای بود که تا بهحال به آن توجه نکرده بود.
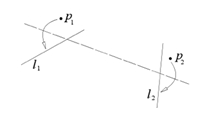
شکل ۱
با پیدا کردن جواب این سؤال، جایزهی دیگری کسب کرد، محبوبیتش بیشتر شد و اصل دیگری برای هندسهاش پیداکرد. اصلی که او را به هندسهی کاغذ و تا امیدوار میکرد. چرا که این اولین اصلی بود که حکمی دربارهی وجود تای خاصی میداد که با خط کش و پرگار امکان پیدا کردنش وجود نداشت! اصل این بود:
۶- برای خطهای $l_1$ و $l_2$، و نقاط $p_1$ و $p_2$، تایی وجود دارد که $p_1$ را بر $l_1$ و $p_2$ را بر $l_2$ منطبق کند. (مگر در مواقعی که....)
آقای ثلاثی معتقد است این مسئله چندان هم سخت نیست! کافی است برای پیدا کردن جواب، دست به کار شوید، روی یک کاغذ دو خط و دو نقطه بکشید و سعی کنید تای مورد نظر را پیدا کنید. این کار را تکرار کنید تا بتوانید حدس بزنید چه مواقعی این کار ممکن است و چه مواقعی بیش از یک تا این کار را می کند.