تولد یک هندسهی نو ؟!
اول از همه اصول اقلیدس را به یاد آورد:
۱- از هر دو نقطه یک خط راست میگذرد.
۲- هر پارهخط را میتوان تا بینهایت روی خط راست امتداد داد.
۳- با یک نقطه بهعنوان مرکز و یک پارهخط بهعنوان شعاع میتوان یک دایره رسم کرد.
۴- همهی زوایای قائمه با هم برابرند. ۱
۵- از یک نقطه خارج از یک خط، میتوان دقیقاً یک خط موازی با خط مفروض رسم کرد.
همهی قضایای هندسهی اقلیدسی، از همین پنج اصل به دست میآمد، و حالا آقای ثلاثی به دنبال این بود که با پیدا کردن چند اصل هندسهی جدیدی را ابداع کند؛ هندسهی کاغذ و تا. برای این کار به این فکر کرد که کارهایی ابتدایی را که با یک بار تا کردن کاغذ میشود انجام داد فهرست کند، اینها را بهعنوان اصول هندسهاش قرار دهد و همهی کارهای ممکن با چندبار تا کردن کاغذ را بهعنوان قضیه از این اصول به دست آورد. برای همین زمانی را صرف امتحان کردن کارهای مختلف با تاکردن برگها کرد.
بعضی از جملهها به وضوح غلط بودند، مثلاً اینکه از «هر سه نقطه روی کاغذ یک تا میگذرد.»
بعضی از جملهها به نظرش درست میآمدند، ولی با کمی تلاش میفهمید اشتباهند. مثلاً اینکه «برای هر دو خط دقیقاً یک تا وجود دارد که آنها را روی هم منطبق میکند.»
بعضی از جملهها درست بودند ولی برای هندسه کارایی نداشتند، مثلاً اینکه «اگر n بار کاغذی را تا بزنیم، حداکثر ۲^n ناحیه روی کاغذ درست میشود.»
بعضیها درست بودند، ولی خیلی هم ابتدایی نبودند و برای نشان دادن درستیشان باید چند بار کاغذ را تا میزد، مثلاً برای این جمله لازم بود دو بار کاغذ تا بشود «برای هر خط و نقطهای خارج از آن، دقیقاً یک تا وجود دارد که از نقطه گذشته و موازی خط باشد.»
در نهایت جملههای زیر را بهعنوان اولین اصول هندسهی کاغذ و تا نوشت: ۲
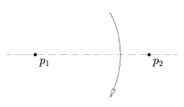
شکل ۱
۱- از هر دو نقطه روی کاغذ، یک تا میگذرد.
۲- برای هر دو نقطه روی کاغذ، دقیقاً یک تا وجود دارد که آنها را روی هم منطبق میکند.
۳- برای هر دو خط روی کاغذ، حداقل یک تا وجود دارد که آنها را روی هم منطبق میکند.
۴- برای هر نقطه و هر خط روی کاغذ، دقیقاً یک تا وجود دارد که از نقطه گذشته و خط را روی خودش منطبق میکند.
۵- .....
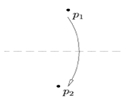
شکل ۲
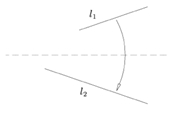
شکل ۳
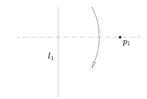
شکل ۴
اما یک سؤال مهم هنوز بدون پاسخ مانده بود: در هر کدام از این اصول، گفته شده که تای خاصی را میشود پیدا کرد، ولی در هر مورد آن تای خاص را میشود با خط کش و پرگار هم پیدا کرد و این اصول را به زبان هندسهی اقلیدسی ترجمه کرد. ۳ پس با استفاده از همین چهار اصل، آقای ثلاثی نمیتواند هر زاویهای را به سه قسمت مساوی تقسیم کند و باید تا آخر عمر در جزیره بماند. حالا سؤال سرنوشتساز آقای ثلاثی این است که آیا میتواند اصول دیگری به این فهرست اضافه کند که هندسهی کاغذ و تا را از هندسهی اقلیدسی متمایز کند؟ آیا میتواند هندسهای قویتر از هندسهی اقلیدسی برای تثلیث زاویه بسازد؟ پیشنهادی در این مورد ندارید؟
۱ اگر خطی به خط دیگری وارد شود و دو زاویهای که با دو طرف آن خط میسازد با هم برابر باشند به آنها زاویهی قائمه میگویند.
۲به نظر شما این جملهها بهعنوان اصول این هندسه مناسبند؟ به اندازهی کافی ساده هستند؟ درستند؟ برای رسمهای هندسی با تا کردن کاغذ کارآمدند؟
۳ در هندسهی اقلیدسی وجود هر کدام از این تاها به چه معناست؟