آشنایی با توپولوژی
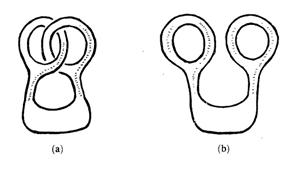
به شکلهای زیر دقت کنید. آیا میتوان شکل (a) را با یک تبدیل پیوسته و بدون پاره کردن، به شکل (b) تبدیل کرد؟
(راهنمایی: پاسخ مثبت است)
با اندکی مسامحه می توان توپولوژی را مطالعهی ریاضی خواصی دانست که با انجام تغییرشکلهای پیوسته، ثـابت میمانند. به عنوان مثال در توپولوژی یک دایره با یک بیضی همارز است.
در کارگاه "آشنایی با توپولوژی" ابتدا مفاهیم مقدماتی توپولوژی بهطور اجمالی مرور شد تا دانشآموزان ببینند این شاخه از ریاضیات با چه اشیا و مفاهیمی سروکار دارد و به چه کارهایی میپردازد. سپس مثالهایی از تغییر شکلهای پیوسته مطرح شد و با کمک چند انیمیشن، شکلها، رویهها و تغییر شکل آنها نمایش داده شد. پس از آن مفاهیم گره و پیوند در توپولوژی معرفی شدند. بعد نوبت به معرفی و مشاهدهی تصویر رویههایی در فضای ۳ و ۴ بعدی رسید و سپس رویههای سازندهی گرهها و پیوندها معرفی شدند. باوجودیکه این شاخه از ریاضی، بسیار مجرد و ذهنی بهنظر میرسد، اما کاربردهای بسیاری در سایر رشتهها دارد؛ در پایان کارگاه برخی کاربردهای نظری گره در فیزیک و بیولوژی اشاره شد تا کاربردی بودن توپولوژی بهتر درک شود.

این کارگاه، شاید سخت ترین کارگاه از نظر دانشآموزان بود؛ اما فرصتی فراهم کرد تا آنها آشنایی مختصری با شاخهای پرکاربرد از ریاضیات پیدا کنند که هیچ پیشزمینهی ذهنی از آن نداشتند و عموما حتی نامی از آن نشنیده بودند. همچنین مواجهی رودررو با شهود ریاضی، عامل دیگری بود که بر پیچیدگیهای این کارگاه افزود. در بحث تغییر شکلهای پیوسته و نیز بحث ساختهشدن گرهها توسط رویهها، تجسم فضایی شکل و حرکت بسیار نیاز است؛ بهرهگیری بهجا از انیمیشینهای متعدد برای نمایش تغییر شکل رویهها، به ایجاد تصویرهای فضایی در ذهن مخاطب، کمک بسیار کرد.
زمستان ۸۹، پروندهای دربارهی توپولوژی روی سایت قرار گرفته است که توضیحات بیشتری دربارهی مطالب کارگاه «آشنایی با توپولوژی» ارائه میدهد و منابعی برای مطالعهی بیشتر معرفی میکند. اگر پرسشی دربارهی مطالب کارگاه دارید با آدرس info@schoolnet.ir تماس بگیرید.