روش مونت کارلو: تاس را بینداز!
گاهی اوقات یک سیستم فیزیکی داریم که میتواند در حالتهای مختلفی باشد. به عنوان مثال، ملکولهای آب را داخل یک لیوان آب در نظر بگیرید. بسته به نوع قرارگیری این ملکولها نسبت به یکدیگر، میگوییم آب در حالت مایع، گاز یا جامد (یخ زده) قرار دارد. پس مکان تمامی ملکولهای ما، میتواند بیانگر حالت سیستم فیزیکی باشد. از این به بعد به نوع مشخصی از چینش ملکولها نسبت به یکدیگر، جواب سیستم و به مجموعهی همهی جوابهای سیستم فیزیکی، فضای جوابها میگوییم.
در خیلی از مسایل برای ما حالت نهایی و یا یک جواب مشخص سیستم فیزیکیمان مهم است، نه راه رسیدن به آن جواب. به عنوان مثال در مورد ملکولهای آب ممکن است برای ما فقط نحوهی چینش ملکولها نسبت به یکدیگر مهم باشد و شیوه یا راه رسیدن سیستم به آن جواب خاص، برایمان اهمیتی نداشته باشد. اگر دقت کرده باشید، دینامیک ملکولی روش شبیهسازیای بود که راه رسیدن به یک جواب سیستم را هم دنبال میکند. به عبارت دیگر، در دینامیک ملکولی، تحول سیستم در گذر زمان مشخص است و قابل بررسی. اما در اینجا روشی را میخواهیم معرفی کنیم که تحول سیستم برایش اهمیتی ندارد. نام این روش، مونت کارلو است. در مونت کارلو، ما در فضای جوابها به طور مستقیم به دنبال جواب مطلوب سیستم فیزیکیمان میگردیم، بدون آنکه درگیر پیچیدگیهای تحول زمانی خود سیستم شویم.
بیایید دوباره به مثال ملکولهای آب برگردیم و شیوهی کار الگوریتم مونت کارلو را بررسی کنیم. اگر N ملکول آب داشته باشیم و هر ملکول را به عنوان یک نقطه در فضای ظرف در نظر بگیریم، با ۳N عدد، میتوانیم مختصات تمامی ملکولهای داخل ظرف را بیان کنیم (۳ تا مختصهی x و y و z برای هر ذره لازم است). پس هر جواب سیستم، یک رشتهی۳N تایی از اعداد است. فضای جوابها هم در واقع مجموعهای از این رشتههای ۳N تایی اعداد است.
فرض کنید میخواهیم ببینیم در یک دمای خاص، به عنوان نمونه دمای ۲۷۰ کلوین (۳ درجه زیر صفر سانتیگراد) ملکولهای آب به چه صورتی در ظرف جای میگیرند. انتظار داریم که آب در این دما یخ بزند. پس جواب درست را هم میدانیم. اما قبل از اینکه ادامه دهیم و ببینیم شبیهسازی مونت کارلو در اینجا به چه کار میآید، باید با یک مفهوم جدید آشنا شویم: پتانسیل لنارد-جونز.
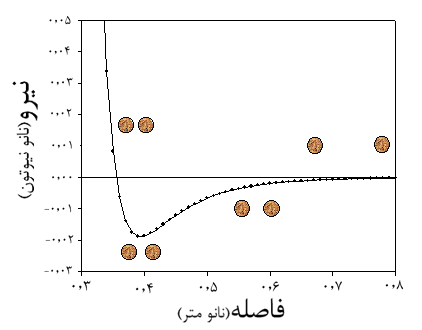
ملکولهای آب، به هم نیرو وارد میکنند. آنها همدیگر را جذب میکنند، تا جایی که فاصلهشان از یک مقدار مشخصی کمتر شود و آن وقت به جای جذب، همدیگر را دفع میکنند. به دلیل همین نیروی دافعه است که ملکولهای آب داخل هم نمیروند و آب را از یک حد مشخصی نمیشود فشردهتر کرد. فیزیکدانها این نیرو را با پتانسیل لنارد-جونز مدل کردهاند. این را گفتم تا معلوم شود که میشود انرژی هر چینش ملکولها یا رشتهی ۳N تایی جواب سیستم را با محاسبهی انرژی پتانسیل لنارد-جونز به دست آورد.
یک اصل بنیادی در فیزیک وجود دارد که میگوید: «هر سیستم فیزیکی، به صورت خود به خودی به سمت وضعیتی حرکت میکند که کمترین انرژی پتانسیل را پیدا کند». در مثال لیوان آب، در واقع باید انتظار داشته باشیم ملکولها، چینشی را انتخاب کنند که انرژی ناشی از پتانسیل لنارد-جونز، کمترین مقدار خود را پیداکند. در دمایی که ما انتخاب کردهایم، با توجه به آنچه ازطبیعت دیدهایم، میدانیم که جواب، همان چینش یخ زدن است.
حالا میتوانیم سیستم فیزیکیمان را با استفاده از الگوریتم مونت کارلو شبیه سازی کنیم. روال کار به این صورت است:
۱- فضای جواب سیستم را مشخص میکنیم: ما این کار را کردهایم. به ازای هر ملکول سه عدد داریم که مختصات x، y، z آن ملکول را مشخص میکند. پس به ازای N ملکول، ۳N عدد هستند که جواب یا حالت سیستم را مشخص میکنند. پس فضای جواب ما مجموعهای از رشتههای ۳N تایی اعداد است.
۲- شیوهی قدم زدن یا جستجو در فضای جواب را مشخص میکنیم: از یک جواب تصادفی (یک چینش تصادفی N مولکول در ظرف) شروع میکنیم. سپس یک ملکول را به صورت تصادفی انتخاب کرده و جایش را عوض میکنیم. اینطوری به یک چینش یا جواب جدید میرسیم.
۳- قدم تصادفی برداشته شده در فضای جواب، یا پذیرفته میشود یا رد میشود: خب حالا که قدم تصادفی را در فضای جوابها برداشتیم و به یک جواب جدید برای سیستم رسیدیم، این سوال پیش میآید که آیا این جواب جدید را بپذیریم یا نه؟ برای این کار از مفاهیم مکانیک آماری استفاده میشود.
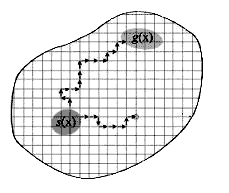
برای این کار کمیتی را محاسبه میکنیم که نشاندهندهی احتمال پذیرش جواب جدید (چینش جدید ملکولها نسبت به یکدیگر) است. ۱ این کمیت، یک عدد بین صفر و یک به ما میدهد. اگر انرژی قدم جدید کمتر از انرژی حالت قبل از قدم زدن باشد، یعنی ما به سمت کاهش انرژی سیستم قدم برداشتهایم (میل طبیعی سیستمهای فیزیکی)، و در این صورت قدم جدید را میپذیریم. اما اگر اینطور نباشد، هر قدر کمیتی که محاسبه کردیم بزرگتر باشد شانس پذیرش قدم بیشتر میشود. در این حالت یک عدد تصادفی بین صفر و یک تولید میکنیم (در واقع یک جور تاس میاندازیم). اگر عدد تصادفی کوچکتر از احتمال محاسبه شده بود، قدم را میپذیریم و سیستم وضعیت جدید را اختیار میکند. اگر نه، به وضعیت قبل از قدم زدن برمیگردیم.
۴- به مرحلهی ۲ بر میگردیم: این حلقه تا زمانی تکرار میشود که سیستم به وضعیت مطلوبی برسد.
اگر یک برنامهی کامپیوتری بنویسیم که ظرف آب ما را شبیهسازی کند چه نتیجهای خواهیم گرفت؟ خب امتحانش کار سختی نیست. توصیه میکنم شکل پتانسیل لنارد-جونز را در ویکیپدیا ببینید تا بتوانید این برنامه را بنویسید. اتفاقی که میافتد این است که با توجه به دمایی که مشخص کردهایم، در هر قدم چینش ملکولها تغییر میکنند و بعد از تعداد مشخصی قدمزدن تصادفی در فضای جوابها، به چینشی میرسیم که شبیه یک ساختار بلوری (همان فاز جامد یا یخ زده) خواهد بود.
۱ این کمیت $e^{\beta\times\Delata{E}}$ است که $\Delta{E}$ اختلاف انرژی بین این جواب جدید و جواب قبل از قدم زدن سیستم است. $\beta$ هم برابر با معکوس حاصلضرب ثابت بولتزمن (یک عدد ثابت در دنیای فیزیک) در دمای سیستم است.