کمی بیشتر پیش برویم...
حالا که تقریباً با مفهوم اتوماتون آشنا شدیم میتوانیم مثالهای پیچیدهتری را از روش رمزنگاری آلمانیها بررسی کنیم.
برای مثال چهطور است فرض کنیم پیامهای معنیدار، با یک «-» شروع میشود و با یک «.» پایان مییابد. یعنی این پیام
-. -. -.... -.. --.. --. -.. ---.. -. -. -. -. ---. --. -.. --. --------. --.. -. -. -..
معنیدار است. (که بیشتر به پیام عقبنشینی شبیه است)
در عوض این یکی پیام
-. -. -.... -.. --.. --. -.. ---.. -. -. -. -. ---. --. -.. --. --------. --.. -. -. -. -
و همچنین این یکی
.. -. -.... -.. --.. --. -.. ---.. -. -. -. -. ---. --. -.. --. --------. --.. -. -. -..
بیمعنی هستند.
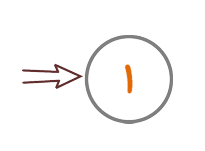
شکل ۶
با اینکه شکل ظاهری این پیامها ترسناک است، این اتوماتون زیاد هم سخت نیست. بیایید ابتدا مانند قبل، دایرهای برای حالت آغازین بکشیم و نام آن را حالت ۱ بگذاریم. برای نشان دادن مکان شروع، همچون قبل، پیکانی از بیرون شکل به داخل دایره میکشیم.
میدانیم که ما فقط با کلماتی سر و کار خواهیم داشت که با «-» شروع شوند، و کلماتی که با «.» شروع میشوند در همان ابتدا رد شدهاند. پس قبل از هر چیز، دو حالت جدید برای ماشین تعریف میکنیم، حالت۲ کلماتی که حرف اولشان «.» است و حالت۳ کلماتی که حرف اولشان «-» است.
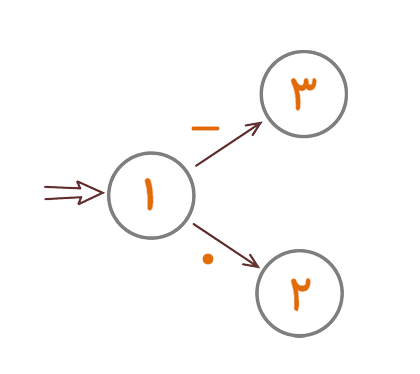
شکل ۷
اول تکلیف کلماتی را که با «.» شروع میشوند روشن میکنیم. همهی این کلمات باید به چراغ قرمز برخورد کنند. میتوانیم برای رسیدن به چنین منظوری به شکل زیر عمل کنیم.
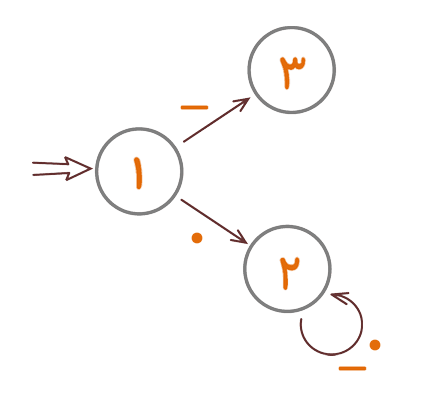
شکل ۸
کلماتی را که با «.» شروع میشوند، در اتوماتون بالا امتحان کنید. جواب داد، نه؟ به عبارتی این کلمات در حالت ۲ گیر افتادهاند و راهی برای خارج شدن از این حالت ندارند. به چنین وضعیتی اصطلاحاً «تله» میگوییم.
اکنون به بقیهی کلمات بپردازیم. طبق الگو این کلمات همه با «-» شروع میشوند. از این دسته کلمات آنهایی چراغ را سبز میکنند که به «.» ختم شوند. برای این گروه حالتی جدید میکشیم و اسم آن را حالت ۴ میگذاریم. مثل قبل، این حالت را با دو دایرهی داخل هم مشخص میکنیم.
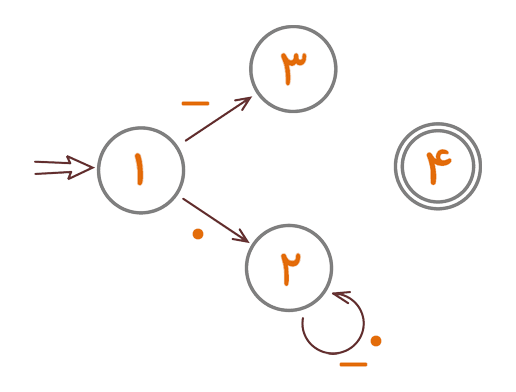
شکل ۹
باید با یک «.» به این حالت جدید رسید. پس پیکانی از حالت ۳ به حالت ۴ میکشیم و روی آن مینویسیم «.». در این صورت پیامهایی که به «.» ختم شوند به حالت ۴ میروند و چراغ سبز میشود. در حقیقت اگر پیام با دو یا سه یا حتی تعداد بیشتری «.» نیز تمام شود چراغ باید سبز شود. پس پیکانی از حالت ۴ به خودش میکشیم و روی آن مینویسیم «.».
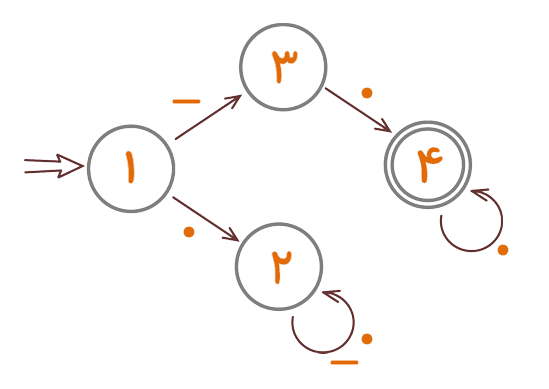
شکل ۱۰
به اتوماتون بالا توجه کنید. در حال حاضر این اتوماتون پیامی را میپذیرد که با یک «-» شروع شود و بقیهی سیگنالهای آن «.» باشد. باید تدبیری بیندیشیم که با اضافه شدن سیگنالهای دیگر بین «-» ابتدای پیام و «.» انتهای پیام همچنان ماشین چراغ سبز را روشن کند. اولین راهحلی که به ذهن میرسد کشیدن یک پیکان با دو سیگنال «.» و «-»، از حالت ۳ به خودش است، به شکل زیر:
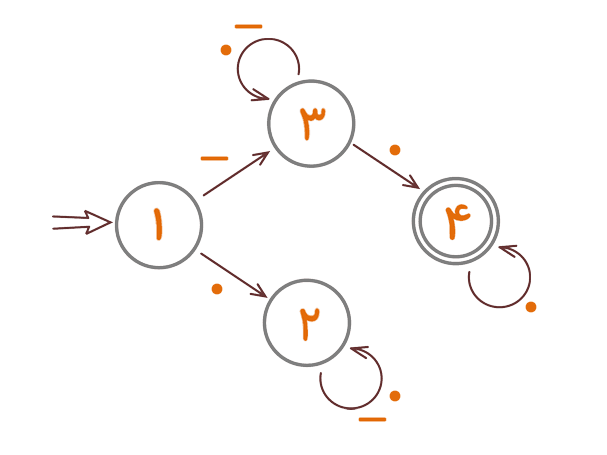
شکل ۱۱
در این صورت از حالت ۳ دو راه با «.» وجود دارد. یعنی وقتی ماشین در حالت ۳ است و یک سیگنال «.» دریافت میکند، میتواند از دو مسیر حرکت کند که یکی به حالت ۳ منجر میشود و دیگری به حالت ۴. به چنین ماشینی، اتوماتون غیر قطعی گوییم.
در واقع دو نوع ماشین داریم: قطعی و غیر قطعی
همانطور که حتماً حدس زدید، اتوماتونی که در صفحهی اول ساختیم قطعی بود. یعنی برای هر سیگنال دریافتی فقط یک مسیر در ماشین وجود داشت.
به زودی میبینید که ماشینهای غیر قطعی به ماشینهای قطعی قابل تبدیل هستند.
گفتیم ماشین با سیگنالهایی به شکل «-.» دو مسیر برای حرکت خواهد داشت:
- حالت ۱ ---> حالت ۳، حالت ۳ ---> حالت ۳
- حالت ۱ ---> حالت ۳، حالت ۳ ---> حالت ۴
همانطور که میبینید تنها یکی از این دو روش به چراغ سبز ختم میشود؛ در صورتیکه پیام بالا، طبق الگو، پیامی معنیدار است. پس لازم است تغییراتی در ماشین بدهیم.
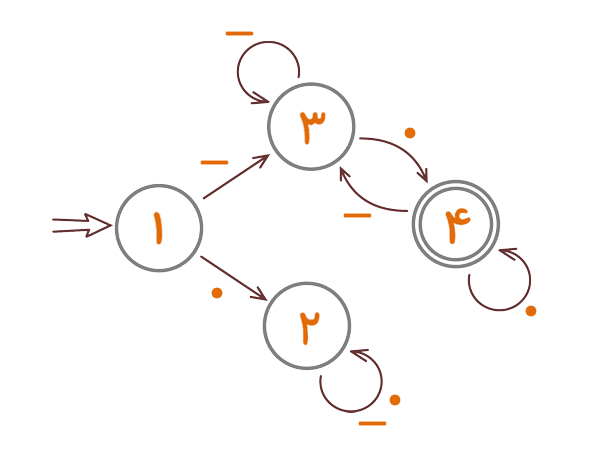
شکل ۱۲
خوب تبریک میگویم! ما موفق شدیم به کمک هم یک ماشین دیگر هم بسازیم و به تورینگ و همکارانش کمک کنیم. همان طور که میبینید، در اتوماتون بالا مشکل قبلی حل شده است.
دقت کنید که ماشین جدید قطعی است. پس دیدیم که ماشینهای غیر قطعی به ماشینهای قطعی قابل تبدیل هستند.
فعالیت.
سیگنالهای پیام زیر را یکی یکی در اتوماتونی که ساختیم وارد کنید و رفتار ماشین را مرحله به مرحله بررسی کنید.
-. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -. -
با دنبال کردن حالتها، متوجه خواهید شد که ماشین مرتباً از حالت ۳ به حالت ۴ تغییر حالت میدهد. انگار مسیری دایرهای را میپیماید. چنین مسیری را اصطلاحاً یک چرخه مینامند. میتوانید فعالیت بالا را با سیگنالهای پیام عقبنشینی نیز انجام دهید.
فعالیت.
اکنون سعی کنید به تنهایی ماشینی بسازید و این بار ماشین شما باید پیامهایی را معنیدار بداند که در آن هیچ دو سیگنال «-»ای پشت سر هم نیامده باشد.